Advanced Math SAT: dạng câu hỏi, các kỹ năng cần có, cách làm

Khi chuẩn bị cho kỳ thi SAT, phần Advanced Math (Toán nâng cao) là một trong những phần thách thức nhất đối với nhiều thí sinh. Vậy Advanced Math SAT kiểm tra thí sinh điều gì? Các dạng câu hỏi thường gặp và những  kỹ năng nào cần có để làm tốt phần này? Cùng PREP tìm hiểu tất tần tật về chủ đề này trong bài viết dưới đây nhé!

I. Advanced Math SAT là gì?

Theo College Board, Advanced Math trong kỳ thi SAT là một phần của bài thi Toán, bao gồm các câu hỏi về những khái niệm toán học nâng cao hơn, yêu cầu khả năng giải quyết vấn đề phức tạp hơn so với các phần cơ bản. Những nội dung bao hàm của Toán nâng cao đó là giá trị tuyệt đối, bậc hai, mũ, đa thức, hữu tỉ, căn bậc hai và các phương trình phi tuyến tính khác.

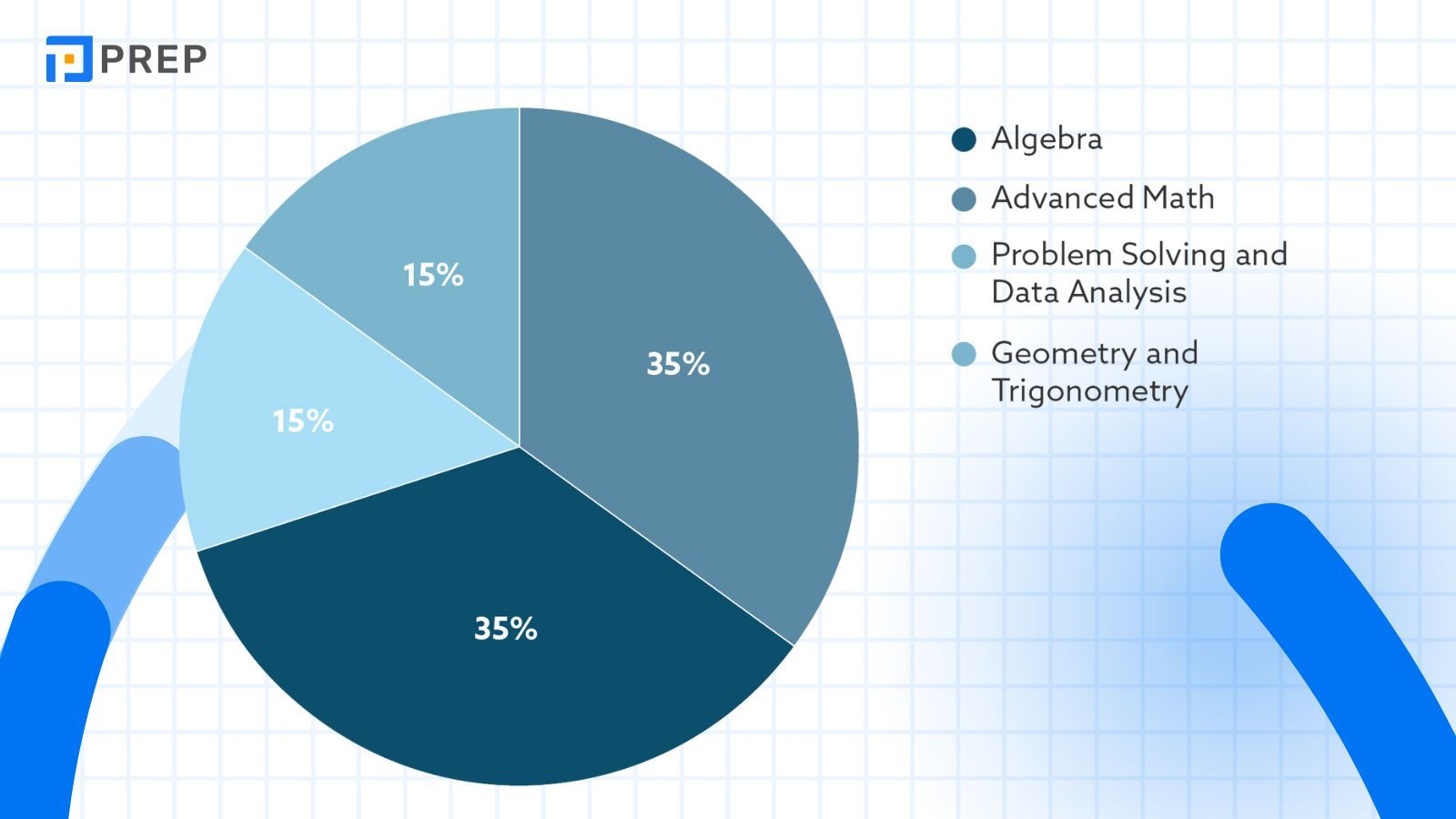
Trong SAT Math, các câu hỏi liên quan đến Advanced Math chiếm khoảng 35% tổng điểm phần Toán (tương đương 13-15 câu). Thí sinh có thể phân bổ khoảng 25 phút cho phần này trong tổng thời gian làm bài 70 phút của phần Toán.

II. Các dạng câu hỏi trong SAT Advanced Math

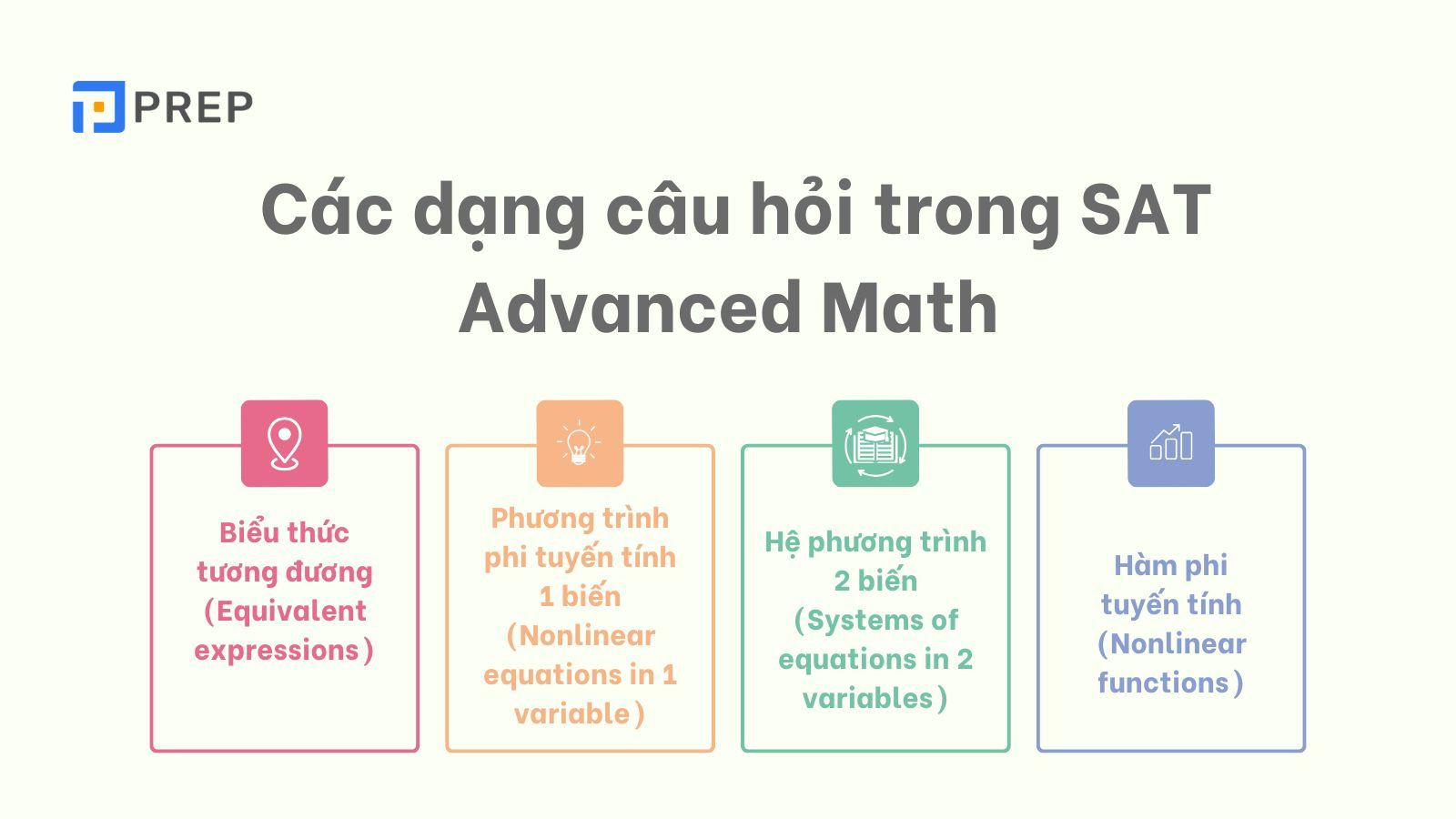
Trong Advanced Math SAT, bạn sẽ gặp các dạng câu hỏi sau:

• Biểu thức tương đương (Equivalent expressions):

  • Dạng câu hỏi này trong Advanced Math SAT yêu cầu bạn biến đổi một biểu thức toán học thành các dạng khác nhau nhưng vẫn giữ nguyên giá trị. Các câu hỏi thường liên quan đến việc rút gọn biểu thức, sử dụng các quy tắc số học, hay áp dụng các định lý để chứng minh rằng hai biểu thức là tương đương.

  • Ví dụ: Cho biểu thức 3 ( 𝑥 + 2 ) − 5 𝑥 3(x+2)−5x. Tìm biểu thức tương đương.

• Phương trình phi tuyến tính 1 biến (Nonlinear equations in 1 variable):

  • Câu hỏi dạng này thường yêu cầu bạn giải các phương trình có chứa biến bậc hai hoặc cao hơn. Phương trình có thể là phương trình bậc hai (quadratic equations), phương trình có căn bậc hai, hoặc các phương trình chứa lũy thừa.

  • Ví dụ: Giải phương trình x2-5x+6=0

• Hệ phương trình 2 biến (Systems of equations in 2 variables):

  • Với dạng câu hỏi này trong Advanced Math SAT, đề bài sẽ yêu cầu bạn giải hệ phương trình với hai ẩn số. Bạn cần tìm giá trị của cả hai biến thỏa mãn điều kiện của cả hai phương trình.

  • Các phương pháp được dùng để giải dạng này đó là phương pháp thế (substitution method) hoặc phương pháp cộng trừ (elimination method).

  • Ví dụ: Giải hệ phương trình: 2x+y=7; x−y=3

• Hàm phi tuyến tính (Nonlinear functions):

  • Dạng câu hỏi cuối cùng của phần Advanced Math SAT đó là hàm phi tuyến tính. Đối với những câu hỏi này, bạn sẽ làm việc với các hàm số phi tuyến tính, chẳng hạn như hàm bậc hai (quadratic functions), hàm số mũ (exponential functions), hoặc hàm bậc ba (cubic functions). Nhiệm vụ của bạn là vẽ đồ thị, xác định các giá trị quan trọng như điểm cực đại, cực tiểu, hoặc tìm nghiệm của hàm số.

  • Ví dụ: Cho hàm số f(x)=x2-4x+3. Tìm giá trị của  f(x) tại x=2

III. Những kỹ năng cần có để làm SAT Advanced Math hiệu quả

Để làm tốt phần SAT Advanced Math, bạn cần phải rèn luyện những kỹ năng sau:

1. Hiểu cấu trúc phương trình

Qua phần thi Advanced Math SAT, College Board muốn đánh giá khả năng của bạn trong việc nắm vững cách các phương trình được hình thành, bao gồm các phần tử như hằng số, biến số, hệ số, và các phép toán (cộng, trừ, nhân, chia, lũy thừa...). Điều này giúp bạn dễ dàng phân tích và giải phương trình một cách hiệu quả.

Chẳng hạn, trong phương trình bậc hai a2+bx+x=0, bạn cần hiểu hiểu rõ các thành phần a, b, c và vai trò của chúng trong việc xác định hình dạng của đồ thị (parabol), cũng như cách giải phương trình bằng cách sử dụng công thức nghiệm.

Hãy cùng xem qua ví dụ cụ thể sau nhé!

If (ax+2)(bx+7)=15x2+cx+14 for all values of x, and a+b=8, what are two possible values for c?

A. 3 and 5

B. 6 and 35

C. 10 and 21

D. 31 and 41

Giải:

Biến đổi vế trái của phương trình, ta được: (ax+2)(bx+7)=abx2+7ax+2bx+14=abx2+(7a+2b)x+14

Lại có: abx2+(7a+2b)x+14= 15x2+cx+14

Do đó, ta có: ab = 15 và 7a + 2b = c

Theo dữ kiện từ đề bài, ta có a + b = 8. Giải phương trình: ab = 15; a + b = 8 ta được a = 3 and b = 5 , hoặc a = 5 và b = 3.

Thay các giá trị của a và b vào phương trình 7a + 2b = c ta được c = 31 hoặc c = 41

➡ Chọn đáp án D.

2. Mô hình hoá dữ liệu

Mô hình hóa dữ liệu (Modeling data) trong SAT Advanced Math liên quan đến việc sử dụng các phương trình và hàm số để biểu diễn, phân tích, và dự đoán các xu hướng hoặc mối quan hệ trong dữ liệu.

Ví dụ:

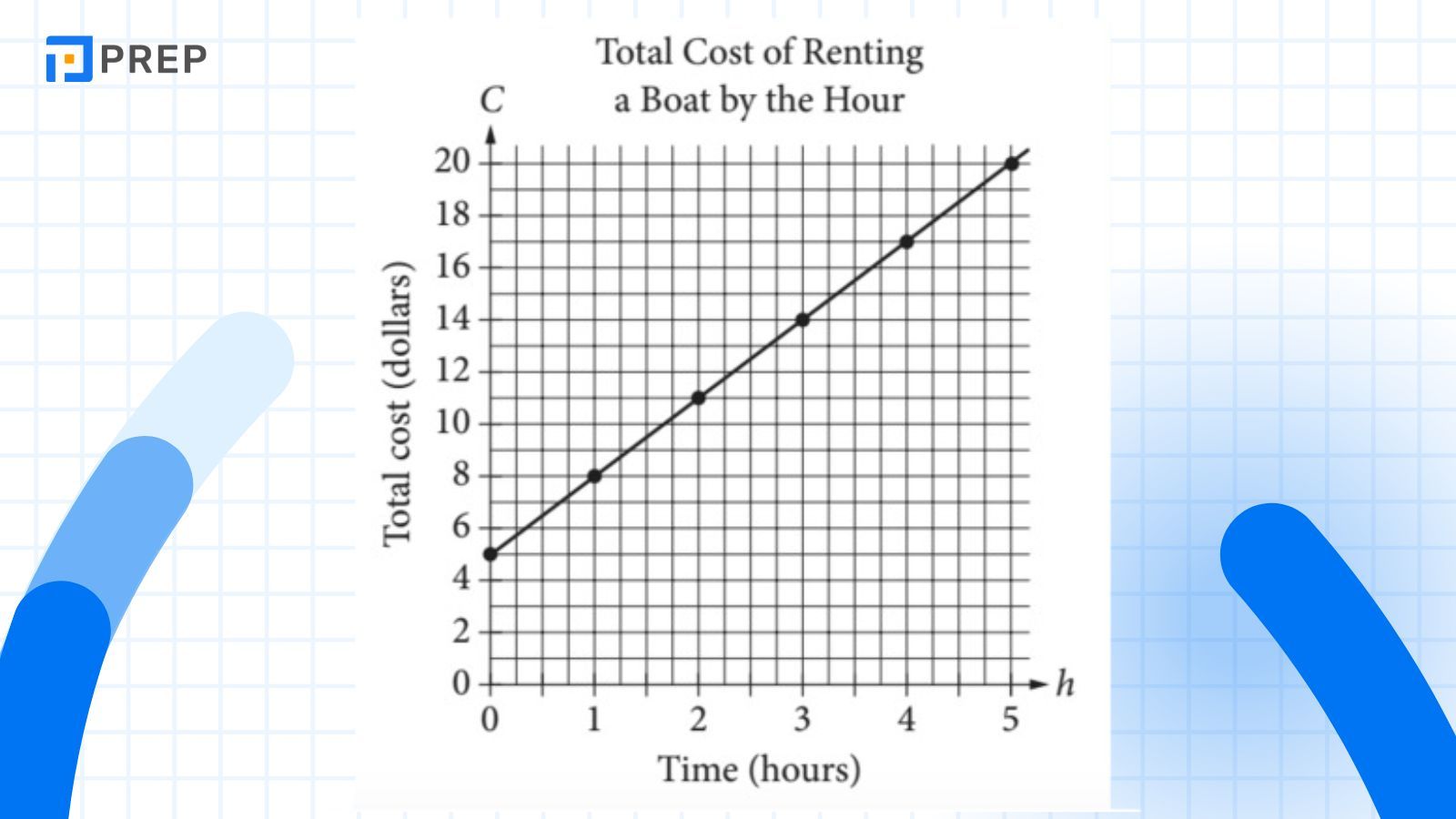
Which of the following represents the relationship between h và C?

A. C=5h

B. C=34h+5

C. C=3h+5

D. h=3C

Giải:

Chúng ta nhận ra rằng C là một hàm số của h và ta đang xét một dạng biến thể của phương trình y = mx + b, trong đó C đóng vai trò như y, và h là x. Để tìm phương trình chính xác cho đường thẳng, ta cần xác định hai yếu tố: hằng số m (độ dốc) và b (giao điểm với trục y).

Khi quan sát đồ thị, ta thấy giao điểm với trục y là 5, do đó đáp án A và D không chính xác. Bây giờ, ta sẽ cần tìm m.

Công thức tìm độ dốc của đường thẳng: m=(y2-y1)(x2-x1)

Chọn 2 điểm (1,8) và (2,11) từ đồ thị và thay nó vào phương trình, ta được: m=11-82-1=3.

Như vậy, với m=3 và y=5, ta được C=3h+5.

3. Biến đổi phương trình

Biến đổi phương trình là một trong những kỹ năng quan trọng khi làm bài thi Advanced Math SAT. Kỹ năng  này liên quan đến việc thay đổi dạng của phương trình mà không thay đổi giá trị của nó.

Ví dụ:

If 3x-52=2x+74+1, solve for x

A. x=214
B. x=14
C. x=18
D. x=118

Giải:

Để giải phương trình có mẫu số, chúng ta nhân cả hai vế của phương trình với bội chung nhỏ nhất của 2 và 4, tức là 4, để loại bỏ mẫu số: 4 x 3x-52=4 x (2x+74+1)

2(3x-5)=2x+11

6x-10=2x+11

4x-10=11

x=214

=> Chọn đáp án A

4. Rút gọn

Kỹ năng rút gọn là khả năng biến đổi các biểu thức phức tạp thành các dạng đơn giản hơn, dễ xử lý hơn trong quá trình giải toán. Điều này bao gồm việc loại bỏ các hạng tử không cần thiết, thu gọn các phép toán và biến đổi phương trình sao cho dễ dàng tìm ra kết quả.

Ví dụ:

(x2y-3y2+5xy2)-(-x2y+3xy2-3y2)

Which of the following is equivalent to the expression above?

A. 4x2y2

B. 8xy2-6y2

C. 2x2y+2xy2

D. 2x2y+8xy2-6y2

Giải:

(x2y-3y2+5xy2)-(-x2y+3xy2-3y2)=x2y-3y2+5xy2+x2y-3xy2+3y2)

=2x2y+3xy2

=> Chọn đáp án C

IV. Cách làm dạng bài Advanced Math trong SAT Math

PREP sẽ hướng dẫn bạn cách làm Advanced Math SAT có thể áp dụng cho gần như các dạng bài. Cùng tìm hiểu ngay nhé!

1. Phân tích yêu cầu đề bài

Trước khi bắt tay vào giải bài toán trong Advanced Math SAT, hãy dành thời gian để đọc kỹ đề bài để xác định rõ loại bài toán bạn đang đối mặt, đó có thể là phương trình bậc hai, phương trình vô tỉ, bất phương trình, hay một bài toán liên quan đến đồ thị hàm số.

Sau đó, hãy tìm hiểu kỹ các yêu cầu của đề bài: cần tìm nghiệm, chứng minh, hay vẽ đồ thị? Nếu bài toán liên quan đến đồ thị, hãy xác định loại hàm số (hàm bậc hai, hàm bậc ba,...) và tìm các đặc điểm quan trọng như tọa độ đỉnh, giao điểm với các trục tọa độ.

2. Lập biểu thức hoặc phương trình

Sau khi nắm rõ yêu cầu của đề bài Advanced Math SAT, hãy bắt tay vào xây dựng phương trình hoặc biểu thức toán học tương ứng. Dựa trên những thông tin đã cho, bạn sẽ cần vận dụng các kiến thức đã học như: quy tắc cộng trừ đa thức, nhân chia đa thức, hay các công thức biến đổi. Đối với hệ phương trình, hãy lập từng phương trình một và xác định số lượng ẩn cần tìm để đưa ra phương án giải hợp lý.

Lưu ý: Hãy tận dụng tối đa những dữ kiện từ đề bài. Thường thì không có dữ kiện nào là thừa trong một bài toán. Do đó, nếu bạn đã làm xong bài Advanced Math SAT mà vẫn chưa sử dụng đến thông tin nào đó thì hãy xem lại nhé!

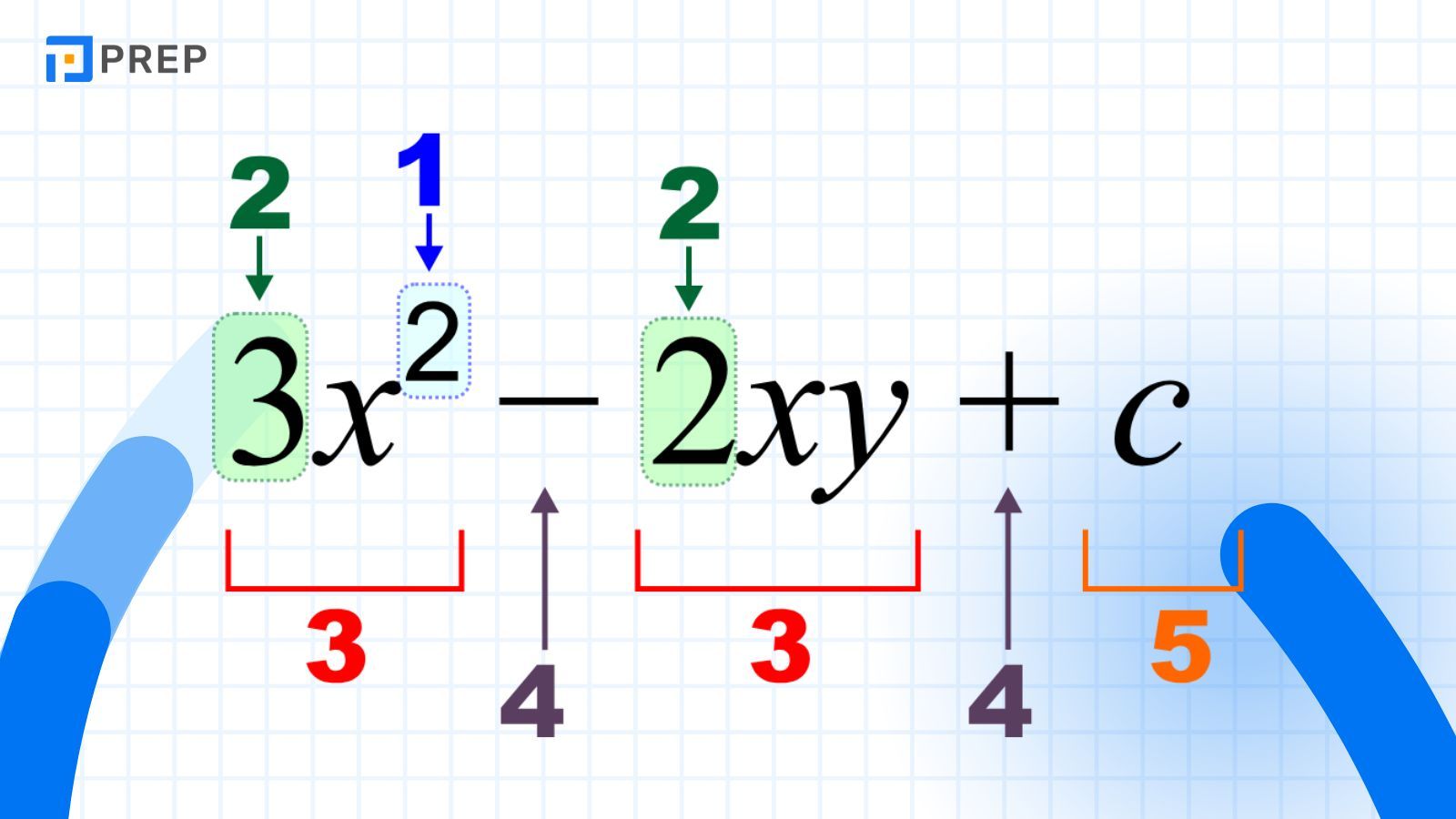
3. Giải phương trình hoặc biểu thức

Sau khi xây dựng phương trình hoặc biểu thức, hãy bắt tay vào giải quyết bằng cách thực hiện các phép toán cần thiết. Bạn có thể cần sử dụng những kỹ thuật như phân tích đa thức thành nhân tử, đặt ẩn phụ để đơn giản hóa biểu thức, hoặc khai triển các đa thức. Đối với các bài toán trong Advanced Math SAT liên quan đến hàm số, hãy vận dụng linh hoạt các kiến thức về đạo hàm, tính đơn điệu, cực trị để tìm ra lời giải.

4. Kiểm tra kết quả và đối chiếu với đề bài

Sau khi tìm ra đáp án, hãy dành thời gian kiểm tra lại từng bước giải của mình để đảm bảo không có sai sót nào xảy ra. Đối chiếu kết quả với yêu cầu của đề bài trong Advanced Math SAT để chắc chắn rằng bạn đã trả lời đúng yêu cầu của bài toán. Nếu có thể, hãy thử thay thế đáp án vào phương trình hoặc biểu thức ban đầu để kiểm tra lại tính chính xác của nó nhé!

V. Các bài tập Advanced Math SAT kèm giải thích chi tiết

Cùng PREP làm một số Advanced Math SAT Practice kèm lời giải thích chi tiết nhé!

1. Bài tập 1

Solve the equation 2x-3x+2=3x+42x-1

Giải:

Nhân chéo ta có:

(2x-3)(2x-1)=(3x+4)(x+2)4x2-8x+3=3x2+10x+8

x2-18x-5=0x=183442

Vậy x=183442

2. Bài tập 2

The boiling point of water at sea level is 212 degrees Fahrenheit (°F). For every increase of 1,000 feet above sea level, the boiling point of water drops approximately 1.84°F. Which of the following equations gives the approximate boiling point B, in °F, at h feet above sea level?

A. B=212-1.84h

B. B=212-(0.001.84)h

C. B=212h

D. B=1.84(212)-1000h

Giải:

Bài toán cho biết điểm sôi của nước ở mực nước biển là 212°F. Mỗi khi độ cao tăng thêm 1000 feet, điểm sôi giảm khoảng 1.84°F. Nhiệm vụ của chúng ta là tìm phương trình biểu diễn điểm sôi B theo độ cao h (tính bằng feet).

Với mỗi 1,000 feet, điểm sôi giảm 1.84°F, vậy cứ 1 foot tăng thêm thì điểm sôi sẽ giảm: 1.841000=0.00184oF

Như vậy, khi tăng thêm h feet, điểm sôi giảm: 0.00184hoF

Với ​​điểm sôi ban đầu là 212°F và nó giảm đi theo độ cao h thì ta có phương trình: B = 212 − 0.00184h

=> Chọn đáp án B

3. Bài tập 3

A farmer sold 108 pounds of produce that consisted of z pounds of zucchini and c pounds of cucumbers. The farmer sold the zucchini for $1.69 per pound and the cucumbers for $0.99 per pound and collected a total of $150.32. Which of the following systems of equations can be used to find the number of pounds of zucchini that were sold?

A. z + c = 150.32

1.69z + 0.99c = 108

B. z + c = 108

1.69z + 0.99c = 150.32

C. z + c = 108

0.99z + 1.69c = 150.32

D. z + c = 150.32

0.99z + 1.69c = 108

Giải:

Chúng ta có các thông tin sau:

• Tổng cộng 108 pounds sản phẩm, bao gồm z pounds bí xanh (zucchini) và c pounds dưa chuột (cucumbers), tức là: z+c=108

• Giá bí xanh là $1.69/pound và dưa chuột là $0.99/pound. Tổng số tiền thu được từ việc bán cả hai là $150.32, tức là: 1.69z + 0.99c = 150.32

Do đó, hệ phương trình biểu diễn số lượng bí xanh và dưa chuột được bán là:

1.69z + 0.99c = 150.32 và z+c=108

Vậy đáp án đúng là B.

Nếu bạn muốn tham khảo nhiều SAT Advanced Math Practice hơn, bạn có thể vào website của CrackSAT hoặc tải về các bài tập TẠI ĐÂY.

Trên đây, PREP đã chia sẻ cho bạn tất tần tật về Advanced Math SAT, từ khái niệm, các dạng câu hỏi đến những kỹ năng cần có và các bài luyện tập. Hy vọng những thông tin hữu ích trên đây sẽ giúp bạn làm chủ được phần thi này.